Am 27, Dezember 1571 wurde Johannes Kepler in Weil der Stadt geboren. Ich halte ihn für einen der größten Wissenschaftler, welche die Menschheit je hervorgebracht hat. Er lebte und wirkte in einer schwierigen Zeit und er mußte in seinen Leben eine Vielzahl von Schicksalsschlägen hinnehmen. Man kann ihn wie sein Zeitgenosse Galileo Galilei als einen Wegbereiter einer neuen Zeit betrachten, in der wissenschaftliche Erkenntnisse und deren Umsetzung in Technologien die Menschheit mehr vorangebracht haben als die vielen Tausend Jahre davor.
Wer sich über das Leben von Johannes Kepler informieren möchte, schaue in der Wikipedia nach oder in folgenden, (da schon älter) kostenlosen Büchern (Google Books):
Carl Gustav Reuschle - Kepler und die Astronomie (1871)
Johannes Kepler - der große Astronom Deutschlands in seinem Leben, Wirken und Leiden (1866)
v. Breitschwert - Johann Keppler's Leben und Wirken nach neuerlich aufgefundenen Manuscripten (1831)
Keplers Name ist unzweifelhaft mit seinen drei Planetengesetzen verbunden, deren Kenntnis heute eigentlich zur Allgemeinbildung gehören sollte. Auf der Hochschule lernt man sie auf einem Blatt Papier aus den Newtonschen Axiomen abzuleiten. Das vernebelt etwas die Leistung Keplers. Denn er mußte sie noch mit unendlichem Fleiß und so gut wie ohne technischen und mathematischen Hilfsmitteln (die Logarithmenrechnung, mit der man schwierige Multiplikationen und Divisionen auf einfache Additionen und Substraktionen zurückführen konnte, war noch in ihren Anfängen) aus den sich über viele Jahre hinziehenden Beobachtungsdaten Tycho Brahes (insbesondere dem Mars betreffend) deduzieren. Was das bedeutet, kann man in Keplers Hauptwerk "Astronomia Nova" von 1609 nachlesen. Und ich habe es vor einiger Zeit getan (in der Übersetzung von Max Caspar) - und es war eine äußerst schwierige und anspruchsvolle Lektüre. Und aus diesem Buch möchte ich ein Thema herausgreifen, welches mit Keplers Namen für immer verbunden ist: die Kepler-Gleichung. Sie ist die grundlegende Gleichung der sogenannten Ephemeridenrechnung, die dazu dient, aus gegebenen Bahnelementen eines Himmelskörpers seine Position am Himmel für beliebig vorgegebene Zeitpunkte zu berechnen.
Johannes Kepler führt diese Gleichung im 60. Kapitel ein, welches da heißt: "Verfahren, aus unserer physikalischen, das heißt richtigen und wahren Hypothese beide Teile der Gleichung und die richtigen Abstände zu berechnen, was beides auf einmal bisher mit der stellvertretenden Hypothese nicht möglich war; ein Beweis für die Falschheit dieser Hypothese".
Johannes Kepler entwickelt in diesem Kapitel - wie überall in seinem Buch - seine Gedankengänge ausschließlich geometrisch-beschreibend, was den mehr analytischem "Denken" der modernen Physik etwas entgegen läuft. Um sie leichter verstehen zu können, werde ich sie deshalb hier in gewohnter Weise formelmäßig darlegen.
Entsprechend der Abbildung ist F der Brennpunkt der Bahnellipse (in der sich die Sonne befindet). P ist die Position des Planeten zum Zeitpunkt t, wobei der Zeitnullpunkt t0 durch die Bedingung festgelegt ist, daß sich der Planet zu diesem Zeitpunkt am Ort B (dem Perihel), befindet (daß Kepler diesen Punkt in den Aphel A gelegt hat, spielt für die folgenden Überlegungen keine Rolle). Für einen kompletten Umlauf benötigt der Planet die Zeit T. E ist die exzentrische Anomalie und φ die wahre Anomalie.
Das Zweite Keplersche Gesetz besagt, daß die Verbindungslinie (FP) in gleichen Zeichen gleiche Flächen überstreicht. Das heißt, mit der Ellipsenfläche (πab) muß offensichtlich
gelten. Das Problem, vor das sich Kepler gestellt sah, bestand in der konkrete Bestimmung der Fläche A(t) des durch die zwei Sehnen (FP) und (FB) sowie dem Kreisbogen (BP) begrenzten Dreiecks ⊳BFP, welches durch die Position des Planeten P(t) festgelegt ist.
Er ging nun folgendermaßen vor: Als erstes verglich er die die Flächen der krummlinigen Dreiecke ⊳BFP' und ⊳BFP. Demnach gilt
Zusammen mit dem Dreieck ⊳OFP' erhält man den Kreissektor S(BOP'), also
woraus sich mit (a)
ergibt - und das ist die Kepler-Gleichung.
Johannes Kepler gelang es nicht, für diese fundamentale Gleichung eine Lösung zu finden. Ihm waren die Schwierigkeiten, die damit verbunden sind, jedoch völlig klar. Denn er schreibt am Ende des genannten Kapitels:
„Ist jedoch die mittlere Anomalie gegeben, so gibt es keine geometrische Methode, um zur ausgeglichenen („wahre“, M.S.) Anomalie oder zur exzentrischen Anomalie zu gelangen. Denn die mittlere Anomalie ist aus zwei Flächenstücken zusammengesetzt, einem Sektor und einem Dreieck. Während der erstere durch den Exzenterbogen gemessen wird, erhält man das letztere, wenn man den Sinus dieses Bogens mit dem Inhalt des größten Dreiecks multipliziert und die letzten Stellen abschneidet. Allein der Verhältnisse zwischen Bogen und zugehörigem Sinus gibt es unendlich viele. Ist also die Summe beider gegeben, so kann man nicht sagen, wie groß der Bogen und wie groß der Sinus ist, der dieser Summe entspricht, wenn wir nicht vorher ermitteln, wie groß die Fläche ist, die zu einem gegebenen Bogen gehört, d.h. wenn wir nicht Tafeln aufstellen und mit ihnen a posteriori operieren. Dies ist meine Ansicht. Je weniger geometrische Schönheit dem Problem zuzukommen scheint, desto dringender fordere ich die Mathematiker auf, sie sollen mir folgendes Problem lösen:
Wenn der Flächeninhalt von einem Teil eines Halbkreises, sowie ein Punkt auf dem Durchmesser gegeben ist, einen Bogen und einen Winkel an diesem Punkt so zu bestimmen, daß die Schenkel des Winkels und der Bogen die gegebene Fläche umschließen. Oder: Die Fläche eines Halbkreises von einem beliebig gegebenen Punkt des Durchmessers aus in gegebenen Verhältnis zu teilen.
Mir genügt die Überzeugung, daß eine Lösung a priori nicht möglich ist wegen der heterogenen Beschaffenheit von Bogen und Sinus. Wer immer mir aber einen Irrtum und einen Ausweg nachweist, der sei mir ein großer Mathematiker gleich Apollonius.“
Und alle, welche die MINT-Fächer so nicht recht leiden mögen (wie die meisten unserer Energiewende-Politiker), bedenkt die Worte Johannes Keplers:
"Die Mathematik allein befriedigt den Geist durch ihre außergewöhnliche Gewißheit"
Johannes Kepler (1571 - 1630)






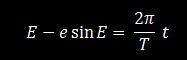
Auch auf den Lebensbahnen von Johannes Kepler lässt sich wandern http://kulturreise-ideen.de/wissenschaft/personen/Tour-johannes-kepler.html
AntwortenLöschen