Wenn die Rotationsachse eines Sterns ungefähr senkrecht zur Blicklinie steht, dann macht sich dessen Eigenrotation in einer typischen Veränderung seiner Spektrallinien bemerkbar. Man kann sich leicht vorstellen, daß in diesem Fall an Stelle einer festen Wellenlänge λ0 quasi ein Strahlungsgemisch aus unterschiedlichen Dopplerverschiebungen gemessen wird, da sich aufgrund der Rotation ein Teil der Sternmaterie mit jeweils unterschiedlichen Geschwindigkeiten auf den Beobachter zu und der andere Teil von ihm weg bewegt. Bezeichnet man mit vr die Radialgeschwindigkeit eines Oberflächenelements am Rand des Sterns, dann wird gemäß dem Dopplereffekt eine Spektrallinie quasi über den Wellenlängenbereich
verschmiert. Genauer, es ändert sich deren um λ0 symmetrisches Profil (Dopplerprofil), welches um so flacher wird, je größer |vr| ist. Dieser wohlbekannte Effekt wird gewöhnlich genutzt, um auf statistischem Weg (wegen der Unbestimmtheit von i in der Beziehung vr sin i) die Rotationsgeschwindigkeit von verschiedenen Sternen in Abhängigkeit von Spektraltyp und Leuchtkraftklasse zu bestimmen.
Bei einer Bedeckung des Sterns durch einen Exoplaneten muß sich demnach abwechselnd die Intensität des blau- und rotverschobenen Anteils verändern, was sich mehr oder wenig deutlich (abhängig von der Bahnlage des Exoplaneten in Bezug auf die Rotationsachse) im Linienprofil niederschlägt. Durch eine genaue Ver-messung dieses Effekts läßt sich die Umlaufrichtung (prograd oder retrogard) des Exoplaneten sowie die Neigung von dessen Bahnebene relativ zur Rotationsachse ermitteln, was ansonsten kaum möglich ist.
Die obige Abbildung zeigt die Auswirkung unterschiedlicher Inklinationen auf die scheinbare Radialgeschwindigkeitskurve. Außerhalb des Transits mißt man aufgrund der Symmetrie des Dopplerprofils einen konstanten Radialgeschwindigkeitswert. Tritt eine Bedeckung ein, ändert sich je nach der Umlaufrichtung zuerst die kurzwellige oder langwellige Flanke der Linie und die scheinbare Radialgeschwindigkeit wird quasi auf eine typische Art und Weise moduliert. Daraus läßt sich die Rotationsrichtung und die Inklination der Exoplanetenbahn bestimmen.
Einstrahlungseffeke und ihre Wirkung auf die Atmosphäre von hot jupiters
„Heiße Jupiter“ sind das Ergebnis einer Migration von Gasplaneten aus dem äußeren Bereich eines Sterns (nur dort können sie entstehen) auf Bahnen in unmittelbarer Sternnähe (z.T. <0.05 AU). Weiterhin erwartet man aus himmelsmechanischen Gründen, daß sich während des Migrationsprozesses die Rotationsdauer immer mehr der Umlaufszeit anpaßt, so daß hot jupiters mit sehr hoher Wahrscheinlichkeit auf ihrer sternnahen Bahn eine gebundene Rotation ausführen. Das bedeutet, daß ihre Tagseite ständig zum Mutterstern und die Nachtseite entsprechend von ihr weg gerichtet ist. Es lassen sich deshalb aufgrund der unterschiedlichen Einstrahlungsverhältnisse auch große Unterschiede in der Strukturierung der Tagseiten-Atmosphäre und der Nachtseiten-Atmosphäre erwarten.
Durch die große Sternnähe überwiegt bei diesen Planeten der Energieeintrag durch Einstrahlung auf der Tagseite bei weitem den Energiefluß, der vom Inneren (d.h. quasi von „unten“) in die Atmosphäre gelangt. Die Auswirkungen dieser Einstrahlung hängen dabei u.a. von der Art des Muttersterns (d.h. dessen spektraler Energieverteilung), der Entfernung des Exoplaneten vom Mutterstern (bestimmt die „Solarkonstante“ S am Ort des Planeten) und natürlich von der Atmosphäre des Exoplaneten selbst ab (Temperatur, chemische Zusammensetzung, Wolkenbedeckung und Art der Wolken, Opazitätsquellen).
Bezeichnet man analog zur Sternphysik mit LP die „Leuchtkraft“ eines Exoplaneten
dann muß sie sich offensichtlich aus zwei Teilen zusammensetzen: Einmal aus der intrinsischen Leuchtkraft Lin , die sich aus den internen Wärmequellen des Exoplaneten speist (z.B. durch Entmischungs- und Kontraktionsprozesse) und zum anderen aus dem Anteil Lds, der aus dem reemittierten Teil der auf der Tagseite absorbierten und thermalisierten Sternstrahlung besteht.
Kann man den intrinsischen Anteil vernachlässigen, dann ergibt sich für die Gleichgewichtstemperatur der Tagseite
Für die effektive Temperatur der sternzugewandten Hemisphäre stellt sich ein Gleichgewichtswert ein, der vom Wert der Solarkonstanten am Ort des Planeten abhängt.
Bezeichnet man mit A die Albedo (5.31), dann ergibt sich aus (5.32) mit L*=4π R*² σT*^4 und dem Abstand a des Exoplaneten zum Mutterstern
Mit dieser Gleichung läßt sich die Tagseitentemperatur eines hot jupiters abschätzen. Eine kurze Überschlagsrechnung mit einem Albedo-Wert von 0.1 (einen derartigen Wert erwartet man bei „heißen Jupitern“ aufgrund der starken Alkali-Absorptionen) ergibt z.B. für HD 189733b einen Wert von ungefähr 1160 K.
Die Größe A ist prinzipiell aus präzisen Transitbeobachtungen, die möglichst ein Sekundärminimum und den Phaseneffekt zeigen sollten, bestimmbar. Das ist dahingehend von Bedeutung, da in dieser Zahl ein Großteil der Physik der sichtbaren Atmosphäre verborgen liegt. Bei den Gasplaneten des Sonnensystems liegt die Albedo zwischen 0.29 (starke Methanabsorption wie bei Neptun) und 0.35 (gut reflektierende Ammoniumhydrosulfid-Wolken auf Jupiter). Bei Exoplaneten muß er aus Atmosphärenmodellen abgeleitet werden. Bei einer Temperatur von 900 K bis 1500 K erwartet man z.B. starke Alkali-Absorptionen, welche den Planeten als sehr dunkel erscheinen lassen. Bei noch höheren Temperaturen (very hot jupiters) können Silizium und einige Metalle in der Planetenatmosphäre auskondensieren und helle, stark das Sternlicht reflektierende Wolken bilden. Entsprechende Atmosphärenmodelle sagen deshalb einen starken Anstieg im Albedo bis auf A~0.55 voraus.
Ausdehnung der Atmosphäre
Exoplaneten vom Typ hot jupiters sind bei vergleichbarer Masse in ihrer Ausdehnung tendenziell größer als „gewöhnliche“ Jupiter. Dieser durch Beobachtungen weitgehend bestätigte Umstand erklärt sich scheinbar zwangslos mit der Aufheizung ihrer Atmosphären durch die intensive Sternstrahlung.
Aufheizung bedeutet, daß ein beträchtlicher Teil der eingestrahlten Energie in Form von Wärmeenergie in der Atmosphäre deponiert wird, was gemäß den Gasgesetzen zu einer Volumenvergrößerung führt. Das Maß der Aufheizung (ausgedrückt durch die effektive Temperatur) hängt dabei neben dem Strahlungsfluß am Ort des Planeten wiederum ganz entscheidend von den Opazitätsquellen in der Atmosphäre ab. Eine Modellierung der Volumenexpansion, die durch Einstrahlungseffekte bedingt ist, ist deshalb nicht ganz einfach. Auch steht die Frage im Raum, ob es durch die asymmetrische Temperaturverteilung zu einer meßbaren Verformung z.B. der 1 bar – Druckisobare über die Tag- und Nachtseite kommt oder ob Temperaturausgleichsmechanismen in der Lage sind, den Temperaturunterschied zwischen den beiden Hemisphären auf wenige 100 K zu begrenzen. Das kann z.B. durch starke Windsysteme geschehen, die von der Eigenrotation des Planeten weitgehend abgekoppelt sind. In solch einem Fall sollte es zu keiner größeren thermisch bedingten Verformung des Gasplaneten kommen.
Tabelle: „hot jupiters“, für die verläßliche Masse- und Radiuswerte ermittelt werden konnten
5.72 Masse-Radius-Beziehung für einige ausgewählte Transit-Planeten vom Typ hot jupiter mit Fehlerbalken. Die intensive Einstrahlung durch den Mutterstern führt offensichtlich zu einem Aufblähen der Planetenatmosphären. © Guillot et.al. 2007
Da ein Gasplanet genauso wie ein Stern keine klar definierte „Oberfläche“ besitzt, muß per Definition festgelegt werden, was man unter seinem „Radius“ überhaupt verstehen soll. Es hat sich dabei bewährt, auf die sinngemäß gleiche Definition wie bei Sternen zurückzugreifen, nämlich auf den Abstand vom Zentrum, wo die (wellenlängenabhängige) optische Tiefe τ (als Maß für die Durchsichtigkeit der Planetenatmosphäre für das Sternlicht, wenn der Gasplanet genau in Sichtlinie mit seinem Mutterstern steht) den Wert 2/3 erreicht hat. Physikalisch entspricht das ungefähr dem Abstand R, wo die tatsächliche Temperatur T(R) genau der effektiven Temperatur Teff des Planeten entspricht. An dieser Stelle hört die Atmosphäre natürlich nicht auf. In Transitlichtkurven beobachtet man einen um ∆R größeren Radius, wobei ∆R ungefähr 5 Skalenhöhen (3.7) entspricht. In der Skalenhöhe einer Atmosphäre ist u.a. über T(h) die thermische Ausdehnung durch Strahlungsabsorption und die damit verbundene Aufheizung explizit mit enthalten.
Man kann nun theoretisch die Entwicklung von ∆R in Abhängigkeit des Alters des Gasplaneten (Entwicklungsmodelle mit Abkühlungsgeschichte – Abkühlung bedeutet Schrumpfung), seiner Migration in sternnahe Bahnen (stetige Vergrößerung von S, Übergang in einen gebundenen Rotationszustand) sowie in Abhängigkeit von Masse und Masseverlust (besonders in Sternnähe durch Jeans-Escape), chemische Zusammensetzung (Metallizität) und der Präsenz eines festen inneren Kerns sowie weiterer Parameter (wie innere Energiequellen) untersuchen.
Ergebnisse
- Die Atmosphärenmächtigkeit hängt empfindlich von der Präsenz eines inneren Kerns (Gestein, „Eis“) und dessen Inhalt an thermischer Energie ab (Bodenheimer at.al. 2003). Das gilt besonders für Exoplaneten mit M≤1 MJ. Eine hohe thermische Trägheit des Kernmaterials verlangsamt den Auskühlungsprozeß und damit das damit verbundene Schrumpfen des Planeten.
- Eine Erhöhung der Metallizität einer H2/He- Atmosphäre begünstigt bei entsprechender Einstrahlung aufgrund des damit einhergehenden Anwachsens der Opazität eine Aufheizung und damit Aufblähung des Gasplaneten. Ohne nennenswerte Einstrahlung verringert dagegen eine Erhöhung der Metallizität nach (3.7) die Skalenhöhe der Atmosphäre und der Planet wird kompakter.
- Die intensive UV-Strahlung vom Mutterstern initiiert photochemische Prozesse, die eine nicht näher bestimmbare Zahl von Molekülarten produzieren, die starken Einfluß auf das Albedo nehmen können (z.B. durch Ausbildung von reflektierenden Dunstschichten). Ihr Einfluß auf die Atmosphärenmächtigkeit ist im Einzelnen jedoch nur schwer einzuschätzen.
Da der Radius bzw. das Masse-Radius-Verhältnis in Korrelation mit der Einstrahlung eine wichtige Beobachtungsgröße ist, kann man versuchen, über Modellrechnungen die Parameterkombinationen zu finden, die diese Beobachtungsgrößen am besten widerspiegeln. Dazu verfolgt man in Entwicklungsmodellen die Abkühlungsgeschichte von Gasplaneten unterschiedlicher Masse, unterschiedlicher chemischer Zusammensetzung (Metallizität), ob mit oder ohne Kern sowie unter unterschiedlichen Einstrahlungsbedingungen und berechnet die Entwicklung des Planetenradius als Funktion der Zeit. Durch Vergleich realer Exo-planetenparameter mit solchen Modellrechnungen läßt sich dann indirekt etwas über deren Natur und Aufbau in Erfahrung bringen.
5.73 Planetenradius als Funktion des Alters für einige besonders große Transit-Exoplaneten, berechnet für den Fall einer 10 mal höheren Metallizität im Vergleich zur Sonne und unter der Annahme, daß sie keinen merklichen Kern und auch keine Wolken in ihrer Atmosphäre besitzen. © A.Burrows et.al. 2007
Masseverlust durch Abdampfung / Jeans-Escape / blow-off
Der hot jupiter HD 209458 b („Osiris“) umkreist seinen Mutterstern (Spektraltyp G0V, Teff~6000 K) in einer Entfernung von lediglich 6.9 Millionen km, was gerade einmal 1/8 der Entfernung des Merkurs zur Sonne entspricht. Der Strahlungsfluß, der ihn auf seiner Tagseite trifft, beträgt etwa 1.1∙10^9 W/m². Durch die damit verbundene enorme Aufheizung (T~1100 K) verliert er aus seiner ca. 10000 K heißen, den Planeten umgebenden ellipsoidförmigen Hülle kontinuierlich Wasserstoff (und natürlich auch andere Elemente), der durch den Sternwind mitgerissen, hinter dem Planeten einen kometenähnlichen Schweif bildet. Er konnte bereits 2003 mit Hilfe des Hubble-Teleskops nachgewiesen werden. Er ließ sich auf der Nachtseite ungefähr einen Planetendurchmesser weit verfolgen (~200000 km).
Berechnungen zeigen, daß „Osiris“ auf diese Weise pro Sekunde etwa 100 bis 500 Millionen kg an Masse verlieren muß. Man vermutet deshalb, daß er über sein geschätztes Alter von 5 Milliarden Jahre bereits 6-7% seiner Masse verloren hat. Eine vollständige Auflösung ist jedoch bei seiner heutigen Bahnlage in absehbarer Zeit nicht zu erwarten. So könnten z.B. ausgedehnte Magnetfelder den Masseabfluß begrenzen, in dem sie Ionen am Entweichen hindern. Der Mechanismus entspricht dabei dem Teilcheneinschluß in der Magnetosphäre der Erde.
Für den kontinuierlichen Masseverlust eines hot jupiters wie HD 209458 b sind mehrere physikalische Prozesse verantwortlich, die alle etwas mit der starken Einstrahlung und der damit verbundenen Aufheizung der oberen Atmosphärenschichten zu tun haben.
Im Einzelnen sind das:
- Thermischer Verlust
Moleküle, deren thermische Geschwindigkeit vth die Entweichgeschwindigkeit
erreicht, können prinzipiell (soweit sie nicht durch Stöße daran gehindert werden) in den freien Weltraum entweichen. Die Rate dN/dt, mit der das geschieht, läßt sich mittels der Jeans-Gleichung (3.34) berechnen, weshalb man auch von „jeans escape“ spricht. Bei den Temperaturen, wie sie in der Exosphäre von stark aufgeheizten Gasplaneten erwartet werden (bis zu einigen 10^4 K), betrifft das die Teilchen, die den hochenergetischen „Schwanz“ der Maxwell-Verteilung (3.29) bevölkern. Aufgrund der gravitativen Bindung hängt die Entweichwahrscheinlichkeit neben der Temperatur T noch entscheidend von der Teilchenmasse m ab: Wasserstoffatome entweichen leichter als Wasserstoffmoleküle und Wasserstoffmoleküle leichter als Heliumkerne usw. Photodissoziationsprozesse, die in die Exosphäre gelangten Moleküle in ihre atomaren Bestandteile zerlegen, können deshalb einen großen Einfluß auf den Teilchenstrom nehmen.
- Verlust aufgrund nichtthermischer Prozesse
Dazu gehört das Mitreißen von geladenen Teilchen aus der oberen Planetenatmosphäre durch den Sternenwind. Dieser Effekt ist um so effektiver, je geringer das Eigenmagnetfeld des Planeten ist. Die Ionenproduktion hängt dabei stark von der Intensität des kurzwelligen Anteils der auftreffenden Sternstrahlung ab.
- Hydrodynamisches blow-off
Bei sehr hohen Temperaturen (10000 – 20000 K) kann die Basis der Exosphäre (d.h. die Höhe, ab der sich Teilchen auf ballistischen Bahnen nahezu stoßfrei bewegen) die Roche lobe des Planeten ausfüllen, wobei die Roche lobe die äußere gravitative Potentialfläche mit dem Potential V=0 darstellt. Über den inneren Lagrangepunkt L1 fließt dann Gas ungehindert in die Roche lobe des Muttersterns ab, was einen kontinuierlichen Masseverlust für den Gasplaneten bedeutet.
5.74 Einer der heißesten bekannten Exoplaneten mit einer effektiven Temperatur von 2500 K ist WASP-12b. Man vermutet (wie auf dieser künstlerischen Darstellung zu sehen), daß er Materie über seinen inneren Lagrangepunkt verliert und sich auf diese Weise eine Gasscheibe um den nur 0.023 AU entfernten Mutterstern (G0, T~6300 K) bildet. © NASA
„Abdampfung“ erfolgt immer aus der Exosphäre eines Planeten. Deren Temperatur sowie deren Abstand zur Roche-Grenze bestimmen im Wesentlichen die Masseverlustrate. Aufgrund der gezeitenbedingten Abweichung der Form der Roche lobe von einer Sphäre erfolgt das Abströmen der Teilchen anisotrop und zwar derart, daß die größten Teilchenflüsse in Richtung des Sterns sowie entgegengesetzt dazu auftreten.
5.75 Gestalt der Exobase eines hot jupiters in der Art von HD 209458b, wie sie aus Modellrechnungen mit einer Exosphärentemperatur von T=11100 K folgt. Die Graustufen kodieren die Entweichraten von (hellgrau) bis (schwarz). Die Achse Stern-Exoplanet verläuft in x-Richtung. © A. Lecavelier des Etangs et.al. 2004
Der Schlüsselprozeß ist dabei die Exosphärenheizung durch die Röntgen- und UV-Strahlung des Muttersterns. Die Temperatur der tieferen Atmosphärenschichten, charakterisiert durch die effektive Temperatur Teff, ist für den Masseabfluß in den Weltraum kaum von Bedeutung. Physikalisch signifikant ist dagegen die um mindestens eine Größenordnung höhere Exosphärentemperatur, die sich als Gleichgewichtszustand zwischen Strahlungsheizung und verschiedenen Kühlmechanismen einstellt.
Auch die Gasplaneten unseres Planetensystems besitzen heiße Exosphären. So beträgt der Unterschied zwischen der Strahlungstemperatur von Jupiter und der Temperatur seiner Exosphäre trotz seiner großen Sonnenentfernung ~500-900 K. Bei hot jupiters rechnet man mit Exosphärentemperaturen von ~1∙10^4 bis ~3 ∙10^4 K für die darin überwiegende Wasserstoffkomponente. Die physikalischen Prozesse, die zur Aufheizung und zu einem fast isothermen Temperaturregime führen, beruhen im Wesentlichen auf der Absorption kurzwelliger Strahlung unterhalb einer Wellenlänge von ungefähr 200 nm sowie in inelastischen Stoß- und Streuprozessen von Röntgen- und Gammaquanten sowie Elektronen, Protonen und leichten Kernen aus dem in die Exosphäre eindringenden Sternwind. Gerade der Einfluß der letzteren Komponente ist bei Exoplaneten nur sehr schwer einzuschätzen, da der Fluß geladener Teilchen in die Planetenatmosphäre stark von einem eventuell vorhandenen Eigenmagnetfeld abhängt. Existiert solch ein Magnetfeld (wie z.B. bei Jupiter), dann kann es anströmende geladene Teilchen ablenken und teilweise in Richtung der Pole kanalisieren, wo es dann im Bereich der Thermosphäre zu Stoßprozessen kommt, bei denen Neutralgasteilchen ionisiert und angeregt, aber auch Moleküle dissoziiert werden. Auf diese Weise läßt sich eine gewisse Menge an zusätzlicher Energie in der Polkalotte eines Exoplaneten deponieren, was effektiv einer Heizung entspricht (auroreal heating). Die dazugehörigen Kühlungsprozesse sind in erster Linie Rekombinationsprozesse, die z.B. in den Polarlichtgürteln von Jupiter und Saturn direkt sichtbar werden. Polare Aufheizungen sollten aber auch zu Windsystemen führen, welche in der Lage sind, die dort deponierte Energie in mittlere und äquatoriale Breiten umzuverteilen.
Die Heizung der Exosphäre durch XUV-Strahlung beruht auf deren hohen Absorptionsquerschnitt für kurzwellige Strahlung und dem Fehlen eines effektiven Kühlmechanismus in dieser Region. Absorptionsquerschnitt und die Häufigkeitsverteilung der absorbierenden Partikel entlang eines Weges in der Atmosphäre bestimmen bekanntlich die optische Tiefe τ als Maß für die Strahlungsabsorption. Ein großer Absorptionsquerschnitt impliziert deshalb, daß die Absorption bereits in der Hochatmosphäre eintritt. Das ist z.B. für die Lyman-Alpha-Absorption von neutralen Wasserstoff (λ=121.6 nm) der Fall. Ist der Absorptionsquerschnitt dagegen gering, dann ist für die optische Tiefe der Konzentrationsterm der absorbierenden Teilchen ausschlaggebend und die Strahlungsabsorption wird erst in tiefer liegenden Atmosphärenschichten wesentlich.
Die Aufheizung auf einige 10^3 bis 10^4 K ist nur dadurch möglich, weil effektive Kühlmechanismen fehlen. In der unteren Atmosphäre erfolgt die Kühlung derart, daß z.B. durch Stöße mit hochenergetischen (d.h. „heißen“) Teilchen Vibrations- und Rotationsfreiheitsgrade von Molekülen angeregt werden, die sie wiederum durch Emission von IR-Strahlung abbauen können. In der wasserstoffdominierten Exosphäre eines Gasplaneten stehen dafür im Wesentlichen nur H3+ -Ionen zur Verfügung. Ihre Konzentration ist aber viel zu gering (die thermische Dissoziation von H2 begrenzt deren Produktionsraten), als daß sie in der Lage sind, einen wesentlichen Kühlungseffekt hervorzurufen.
Weitere Kühlmechanismen, die quantitativ aber nur schwer abzuschätzen sind, betreffen die molekulare Wärmeleitung (H2) in Richtung der kühleren Mesosphäre, die Anregung höherer energetischer Zustände neutraler Wasserstoffatome sowie deren Ionisierung durch Stöße. Außerdem verlassen hochenergetische Teilchen ständig die Exosphäre in Richtung Weltraum, was genau genommen auch nichts anderes als eine Art von Kühlung darstellt. Bei extremer Sternnähe (<0.04 AU) kann sie sehr effektiv werden.
5.76 Berechnete Gleichgewichtstemperaturen für die Exosphäre als Funktion des Abstandes d vom Mutterstern für drei verschiedene Modelle von HD 209458 b, die sich bei einem Abstand von 0.045 AU in ihrer Exosphärentemperatur unterscheiden. Die im XUV absorbierte (minimale) Energiemenge wurde anhand von Modellrechnungen zu 2.7∙(d/1AU) erg cm^(-2) s^(-1) abgeschätzt. Der rapide Temperaturabfall bei einer Entfernung unterhalb von 0.04 AU ist das Resultat einer schnell ansteigenden Entweichrate, was zu einer starken Abkühlung der Exobase führt.
Die Intensität der XUV-Strahlung am Ort des Planeten hängt von der effektiven Temperatur des Muttersterns, d.h. von dessen Spektraltyp ab. Er bestimmt, welcher Anteil der Leuchtkraft auf den hier interessierenden Spektralbereich entfällt. Da die Intensität mit dem Quadrat der Entfernung abnimmt, ist die nächste wichtige Größe der Abstand des Planeten vom Mutterstern. Er kann während eines Umlaufs variieren, wenn die Bahnellipse eine merkliche Exzentrizität aufweist. Will man den Masseverlust im Rahmen von Entwicklungsmodellen untersuchen, muß man darüber hinaus auch noch die stellare Entwicklung der UV-Leuchtkraft in geeigneter Weise in die Modellrechnungen einfließen lassen. Derartige Modellrechnungen wurden mehrfach durchgeführt, um die Beobachtungsergebnisse am Exoplaneten HD 209458 b erklären zu können (z.B. A. Lecavelier des Etangs et.al. 2008). Die dabei berechneten Entweichraten für atomaren und molekularen Wasserstoff sind mit den Beobachtungen (~〖10〗^7 kg s^(-1)) durchaus vereinbar.
Nachweis des Massenverlusts bei Transitbeobachtungen
Genaue Transitbeobachtungen von HD 209458b wurden bereits 2003 von Vidal-Madjar et.al. mit Hilfe des Space Telescope Imaging Spectrograph (STIS, Hubble-Teleskop) durchgeführt mit dem Ziel, neutralen Wasserstoff H I nachzuweisen. Diese Beobachtungen wurden später wiederholt (Lecavelier des Etangs et.al. 2010) und führten zur Entdeckung des bereits beschriebenen intensiven Masseabflusses aus der Exosphäre dieses „Heißen Jupiters“.
Untersucht wurde die Lyman-Alpha-Absorption bei λ=121.6 nm in der Atmosphäre des Exoplaneten während des Transits. Aufgrund der Bedingungen in der Exosphäre (und seiner erwarteten Ausdehnung) kommt nur die Lyman-Alpha-Absorption in Frage, da die Auswirkungen anderer denkbarer Übergänge mit der verwendeten Beobachtungstechnik nicht meßbar sind.
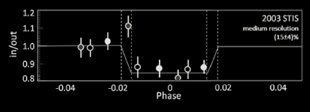
5.77 Die Transitlichtkurve von HD 209458 b zeigt bei Ly-α eine überraschend starke Absorption um 15±4 %, was auf eine ausgedehnte Hülle von neutralem Wasserstoffgas um den Exoplaneten schließen läßt. © Ehrenreich et.al. 2009
Das Ergebnis der Beobachtungen war ein überraschend deutlicher Intensitätseinbruch von ~15% während der Totalitätsphase. Wenn man annimmt, daß der projizierte Radius der Roche lobe ~2.8 Planetenradien beträgt und dieser Bereich mit neutralen Wasserstoff in der theoretisch erwarteten Teilchenzahldichte ausgefüllt ist, dann sollte die Einsenkung der Transitlichtkurve bei Ly-α ~11% betragen. Eine weitere Anomalität zeigte die Untersuchung des Linienprofils der Ly-α - Linie während und außerhalb des Transits. Sie ergaben eine Modifizierung des Dopplerprofils der Linie, aus der sich eine höhere Ausströmgeschwindigkeit als die theoretisch Mögliche mit v=43 km/s aus der Roche lobe heraus lesen läßt. Aus diesen Beobachtungen schließt man im Vergleich mit Modellrechnungen
- Neutrales Wasserstoffgas muß sich auch außerhalb der Roche lobe befinden
- Da die Ausströmgeschwindigkeit, die sich im Linienprofil niederschlägt, größer ist als die Entweichgeschwindigkeit, muß ein Masseabfluß stattfinden
Diese Befunde stehen im Einklang mit einer Masseverlustrate von dm⁄(dt≈(1 bis 5) ∙10^7 ) kg/s. HD 209458 b befindet sich im Zustand des hydrodynamischen blow-off.
Massenverlust und Lebensdauer von hot jupiters
Mit dem stetigen Masseverlust in Verbindung mit einer Migration der Bahn in immer größere Sternnähe stellt sich die Frage der Lebensdauer von Gasplaneten des Typs hot jupiter. Diese Frage umfaßt genaugenommen mehrere Aspekte, die bei einer theoretischen Behandlung ins Kalkül zu ziehen sind:
- Ort der Entstehung des Gasplaneten in der protoplanetaren Scheibe
- Umstände und Dynamik der Migration in immer sternnähere Bahnen
- Physikalische Parameter des Gasplaneten in Abhängigkeit seiner Abkühlungsgeschichte
- Physikalische Parameter des Muttersterns (primär dessen Masse und Metallizität)
- Die Sternentwicklung selbst (zeitlicher Verlauf der Leuchtkraft, Sternwinde und deren Auswirkung auf die Masseverlustrate)
- Intrinsische planetare Magnetfelder in Verbindung mit dem Übergang in einen gebundenen Rotationszustand (tidal locking)
- Entwicklung der Atmosphäre des Gasplaneten unter Strahlungseinfluß
Das sind nur einige Punkte, welche Einfluß auf die Lebensdauer eines Gasplaneten nehmen. Das „Lebensende“ läßt sich dabei je nach Standpunkt als „vollständige Zerstörung“ des Planeten, als Verlust seiner gesamten Atmosphäre (chthonian planets) oder als der weitgehende Verlust seiner leichten Atmosphärengase Wasserstoff und Helium (hot neptunes) definieren.
Simulationsrechnungen zeigen jedenfalls, daß die verbleibende Lebensdauer von hot jupters mit Umlaufszeiten unterhalb von drei Tagen (was ungefähr einem Abstand von ~0.04 AU zum Mutterstern entspricht) deutlich begrenzt ist, wobei sie u.a. durchaus entscheidend von der Masse des Gasplaneten abhängt – je größer die Masse des Exoplaneten ist, desto länger kann er sich einer Erodierung durch die Strahlung seines Muttersterns widersetzen.
5.78 Linien gleicher Lebensdauer t*=log10 (∫dM/(dM/dt)), die sich aus der vollständigen Erosion des Planeten mit der (zeitabhängigen) Massenverlustrate dM/dt ergeben (Modell A in Abb. 5.76). Die Lage von HD 209458b ist durch einen roten Kreis gekennzeichnet. © A.Lecavelier des Etangs, 2004
Hot neptunes
Was den Masseverlust betrifft, sind verschiedene Szenarien denkbar. Verliert der Gasplanet den größten Teil des Wasserstoffgehalts seiner Atmosphäre, dann wird er sich wahrscheinlich zu einem hot neptune entwickeln. Das sind Gasplaneten mit einem ähnlichen stofflichen Aufbau wie Uranus und Neptun in unserem Sonnensystem mit einem signifikanten Defizit an Wasserstoff in den Atmosphärenschichten. Durch ihre Sternnähe sind diese jedoch ähnlich wie bei den die hot jupiters stark aufgeheizt. Ein ernsthafter Kandidat für diese spezielle Gruppe von Gasplaneten ist Gliese 436 b. Er bewegt sich in einer Entfernung von nur 0.03 AU um einen M2.5V-Zwergstern (T~3300 K), wobei er für einen Umlauf 2 Tage und 15.5 Stunden benötigt. Seine effektive Temperatur konnte aus dem Nebenminimum der Transitlichtkurve zu ~700 K bestimmt werden.
Planeten, deren Atmosphären durch exogene Einflüsse fast vollständig erodiert sind, nennt man chthonische Planeten. Dieser Begriff wurde 2003 eingeführt und geht auf das griechische Wort Chthonia zurück, welches sich wiederum von dem Substantiv χθών ableitet, was in der griechischen Mythologie „Erde“ im Sinn der Oberfläche der feurigen „inneren“ Erde bedeutet, dem Ort also, wo der „chthonische“ Gott Hades herrscht. Wenn sich also von einem Gas-, Flüssigkeits- oder Gesteinsplaneten die Atmosphäre durch die Strahlung ihres Muttersterns verflüchtigt hat, dann reiht man ihn in diese hypothetische Klasse von Planeten ein. CoRot-7b im Sternbild Einhorn könnte dazu gehören.















Keine Kommentare:
Kommentar veröffentlichen